Paraboloid with Maximal Volume
by R. Grothmann
We search the paraboloid of maximal volume, which fits inside a cone.
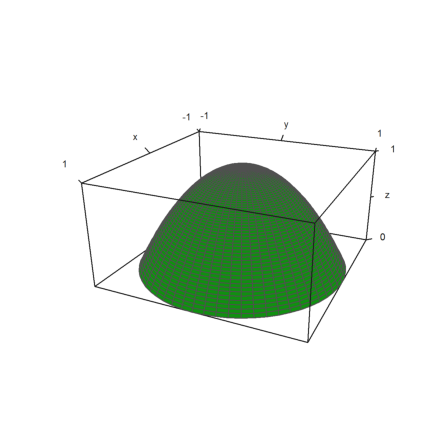
A paraboloid is a parabola y=x^2 rotated around the y-axis. Here is an image.
>plot3d("1-x^2",xmin=0,xmax=1,rotate=2):
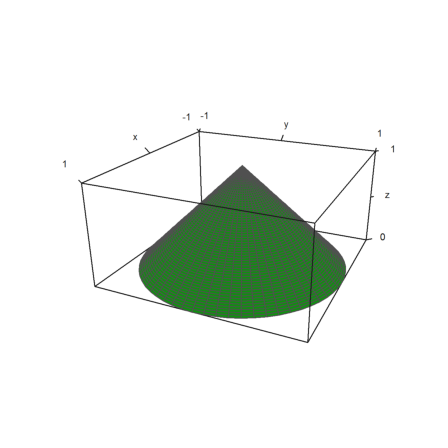
We want to fit such a paraboloid under the cone, which is a the rotated function 1-|x|.
>plot3d("1-x",xmin=0,xmax=1,rotate=2):
We first assume, that the parabola has the form ax^2+b.
>:: function p(x,a,b) := a*x^2+b
2
p(x, a, b) := a x + b
It should touch 1-|x|. So we find all parabolas that touch this function.
>:: solve(diff(p(x,a,b),x)=-1,x), sb := solve(at(p(x,a,b)=1-x,%),a)
1
[x = - ---]
2 a
1
[a = -------]
4 b - 4
We get a family of parabolas.
>:: pt(x,b) := at(p(x,a,b),sb)
2
x
pt(x, b) := ------- + b
4 b - 4
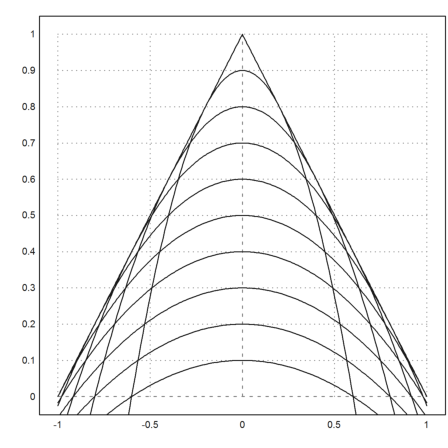
Let us check with plots.
>b=(0.1:0.1:0.9)'; plot2d("1-abs(x)",-1,1); ...
plot2d(mxm("pt(x,b)"),-1,1,add=1):
Now we need to compute the volume of the rotated parabola for y>0. We need to determine the radius of the paraboloid for specific y.
>:: yinv := solve(pt(x,b)=y,x)
2 2
[x = - 2 sqrt(b y - y - b + b), x = 2 sqrt(b y - y - b + b)]
Then we find the volume.
>:: define(F(b),integrate(%pi*rhs(yinv[1])^2,y,0,b))
3 2
F(b) := - 2 pi (b - b )
And maximize it.
>:: solve(diff(F(b),b)=0,b), F(b) | %[1], float(%)
2
[b = -, b = 0]
3
8 pi
----
27
0.93084226773031
Plot this specific parabola.
>plot2d("1-abs(x)",-1,1); plot2d(mxm("pt(x,2/3)"),add=1):
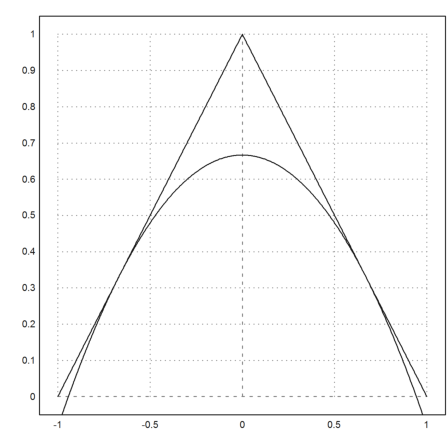
This is our solution.
>:: pt(x,2/3)
2
2 3 x
- - ----
3 4
Now we solve a similar problem. We request, that the parabola must fit under the cone function 1-|x|, and then turn such a parabola around the y-axis.
It is not obvious that the maximal volume is achieved, if the parabola is symmetric. However, think of a parabola which touches 1-|x| in some point x>0. We can assume that the vertex of the parbola is on the positive side. Then we can show that there is a larger parabola, which touches 1-|x| in the same point x, and is symmetric with respect to the y-axis.
However, for the following, we solve the general case numerically, and assume that the parabola has two zeros a, b with
-1 < -b < a < b < 1
and touches 1-x somewhere in [0,b].
>:: function p(x) := c*(x-a)*(x-b)
p(x) := c (x - a) (x - b)
>:: solve(diff(p(x),x)=-1,x); sc := rhs(solve(at(p(x)=1-x,%),c)[1])
2 sqrt((a - 1) b - a + 1) - b - a + 2
- -------------------------------------
2 2
b - 2 a b + a
>:: define(ps(x),at(p(x),c=sc))
ps(x) :=
(2 sqrt((a - 1) b - a + 1) - b - a + 2) (x - a) (x - b)
- -------------------------------------------------------
2 2
b - 2 a b + a
The functions pt are the set of such parabolas. Let us plot a few samples.
>plot2d("1-abs(x)",r=1); ...
a=(-0.9:0.1:0)'; b=0.9; plot2d(mxm("ps(x)"),add=1):
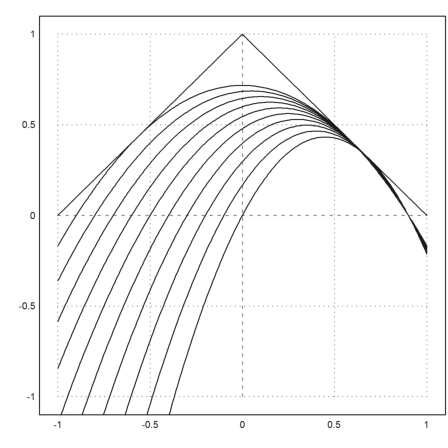
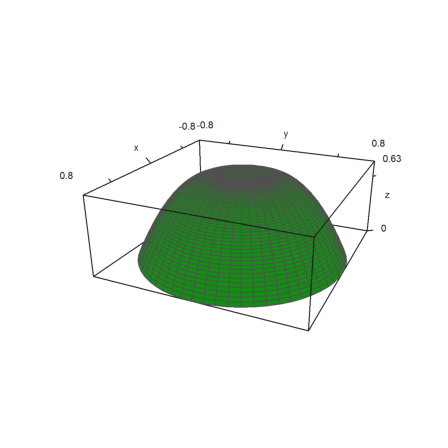
Let us plot such a rotated parabola.
>a=0.8; b=-0.3; plot3d("::ps(x)",xmin=0,xmax=0.8,rotate=2):
To determine the area of the rotated parabola, we integrate with polar coordinates.
>:: integrate(2*%pi*x*ps(x),x); V(a,b) := factor(at(%,x=b))
V(a, b) :=
3
pi b (b - 2 a) (b - 2 sqrt((a - 1) (b - 1)) + a - 2)
- -----------------------------------------------------
2
6 (b - a)
The maximum is the same as before. We take a=-y*x, b=x with 0<x<1 and 0<y<1. The plot shows a maximum with y=1. So we have two symmetric zeros, and get the same case as above.
>plot3d(mxm("V(x,-y*x)"), ...
xmin=0.1,xmax=1,ymin=0,ymax=1,user=1,xlabel="a",ylabel="b",scale=1); ...
insimg;
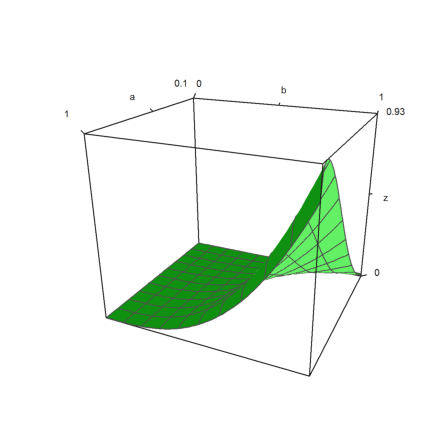
It is not easy to show that V(a,b) increases monotonically as a decreases from 0 to -b. But if we assume this is true, we get the same maximum as before.
However, we have to use Euler's numerical algorihms, since Maxima cannot solve this instantly.
>xmax=fmax(&V(-x,x),0,1); &V(-x,x)(xmax)
0.93084226773